Beyond the Nozzle: The Dramatic Journey of Stagnation Pressure
Stagnation pressure, also known as total pressure or pitot pressure, is a concept in fluid mechanics and thermodynamics. It is a measure of the total energy contained in a fluid stream, accounting for both the static pressure and the kinetic energy of the fluid.
When a fluid (liquid or gas) flows, it possesses both static pressure (pressure exerted by the fluid molecules in random motion) and dynamic pressure (pressure due to the fluid's motion). Stagnation pressure is the sum of these two pressures and represents the maximum pressure that the fluid would achieve if it were brought to a complete stop, adiabatically (without any heat transfer) and isentropically (without any entropy change).
The most common way to measure stagnation pressure is by using a Pitot tube, named after Henri Pitot, a French engineer who invented it in the early 18th century. The Pitot tube is a device with two openings, one facing the fluid flow directly to measure the stagnation (total) pressure, and another opening on the side to measure the static pressure. By subtracting the static pressure from the stagnation pressure, we can determine the dynamic pressure of the fluid flow.
Stagnation pressure is essential in various engineering applications, such as aerodynamics, fluid dynamics, and gas dynamics. It is used to calculate important parameters like flow velocity, fluid density, and total energy in the fluid stream. In many practical situations, the conservation of stagnation pressure is applied to analyze the flow behavior through various components like nozzles, diffusers, and turbines.
Mathematically, stagnation pressure (P_0) can be expressed as:
P_0 = P + 0.5 * ρ * V^2
where: P_0 is the stagnation pressure, P is the static pressure, ρ (rho) is the density of the fluid, and V is the velocity of the fluid flow.
Stagnation pressure is a useful concept for engineers and scientists to understand and analyze fluid flow behavior and energy changes in fluid systems.
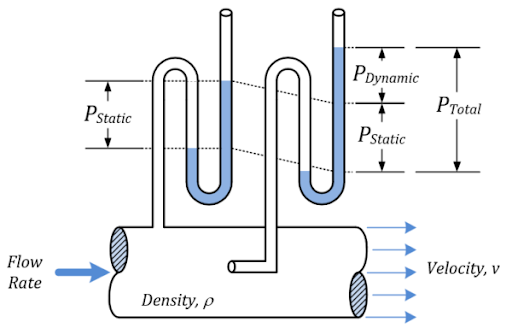
Fig 1. Stagnation pressure
What is stagnation pressure?
Stagnation pressure, also known as total pressure or pitot pressure, is a concept in fluid mechanics and thermodynamics. It refers to the total energy contained in a fluid stream, accounting for both the static pressure and the kinetic energy of the fluid.
When a fluid (liquid or gas) flows, it possesses both static pressure (pressure exerted by the fluid molecules in random motion) and dynamic pressure (pressure due to the fluid's motion). Stagnation pressure is the sum of these two pressures and represents the maximum pressure that the fluid would achieve if it were brought to a complete stop, adiabatically (without any heat transfer) and isentropically (without any entropy change).
Stagnation pressure is a fundamental concept used in various engineering applications, such as aerodynamics, fluid dynamics, and gas dynamics. It is measured using devices like a Pitot tube, which can determine both the stagnation pressure and the static pressure of the fluid flow. Stagnation pressure is critical for analyzing flow behavior, energy changes, and pressure distributions in fluid systems and is used to calculate important parameters like flow velocity, fluid density, and total energy in the fluid stream.
Examine our diverse selection of Pressure Sensor to find the best fit for your specific needs.
Can stagnation pressure be negative?
Stagnation pressure, as a physical quantity, cannot be negative in conventional circumstances. Stagnation pressure represents the total energy contained in a fluid stream and is the sum of the static pressure and the dynamic pressure (0.5 * ρ * V^2). Both static pressure and dynamic pressure are non-negative values, and their sum, the stagnation pressure, will also be non-negative.
However, there are some specific scenarios or conditions in which the stagnation pressure can be mathematically calculated to have a negative value. This usually occurs in theoretical or academic contexts and is not physically meaningful.
One such scenario is in the context of compressible flow through a converging-diverging nozzle. As the flow reaches a point of choking (where the flow velocity reaches the local speed of sound), the pressure downstream of the throat can be calculated to be negative in the theoretical equations. In this case, the negative stagnation pressure represents an extreme situation where the flow becomes supersonic, and certain assumptions used in the equations break down.
It's essential to recognize that such negative values are typically artifacts of the mathematical models or idealizations used in specific theoretical scenarios and do not have a physical interpretation. In real-world applications and practical engineering situations, stagnation pressure will always be a non-negative quantity, representing the total energy in the fluid flow.
What are Stagnation Pressure measuring ways?
Stagnation pressure, also known as total pressure or pitot pressure, can be measured using various methods and instruments. The most common and widely used technique is by employing a Pitot tube. Here are some of the ways stagnation pressure can be measured:
- Pitot Tube: A Pitot tube is a simple and effective device used to measure stagnation pressure in fluid flows. It consists of two openings – one facing the fluid flow directly to measure the total pressure (stagnation pressure), and another opening on the side to measure the static pressure. By comparing the stagnation pressure with the static pressure, the dynamic pressure (velocity pressure) can be determined.
- Pitot-Static System: In aircraft, a Pitot-static system is used to measure both stagnation pressure (pitot pressure) and static pressure. The Pitot tube measures the total pressure, and a static port measures the static pressure. The difference between these two pressures provides the dynamic pressure, which is used to calculate the aircraft's airspeed.
- Pressure Transducers: Modern pressure transducers or pressure sensors can be used to measure stagnation pressure indirectly. By carefully positioning the pressure sensor in the flow, it can measure the total pressure, and the static pressure can be obtained separately using another pressure sensor placed at a point perpendicular to the flow.
- Manometers: U-tube or inclined-tube manometers can be used to measure the difference between stagnation pressure and static pressure. The fluid levels in the tubes respond to the pressures applied at their respective ends, allowing for pressure difference measurements.
- Pressure Gauges: Specialized pressure gauges, such as differential pressure gauges, can measure the difference between the stagnation pressure and static pressure.
- Pitot-Static Tubes: These are similar to Pitot tubes but also include additional openings to measure the static pressure simultaneously. They are commonly used for measuring airspeed in aircraft and wind speed in meteorological applications.
- Electronic Pressure Probes: These probes can measure pressure at different points in a flow field, including stagnation pressure, and provide real-time data for analysis and measurements.
It's important to note that the choice of the measuring method depends on the specific application, the accuracy required, the nature of the fluid flow, and the available instrumentation. For most practical purposes, Pitot tubes and Pitot-static systems remain the most commonly used methods for measuring stagnation pressure in various engineering and aerodynamic applications.
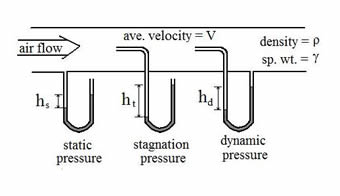
Fig 2. Stagnation Pressure
Stagnation Pressure formulas
Stagnation pressure, denoted as P_0, is the sum of the static pressure (P) and the dynamic pressure (q) of a fluid flow. The dynamic pressure is defined as one-half of the fluid's density (ρ) times the flow velocity squared (V^2). The formula for stagnation pressure can be expressed as:
P_0 = P + 0.5 * ρ * V^2
Where: P_0 = Stagnation pressure (total pressure or pitot pressure) P = Static pressure ρ (rho) = Density of the fluid V = Flow velocity
This formula is applicable to both compressible and incompressible fluid flows, provided that the flow is adiabatic (no heat transfer) and isentropic (no entropy change). Stagnation pressure is an important parameter in fluid mechanics and is used in various engineering applications to analyze fluid flow behavior, energy changes, and pressure distributions.
An example of using these formula
Let's walk through an example of using the stagnation pressure formula to calculate the total pressure at a specific point in a fluid flow.
Example: Suppose we have an air duct with a flow velocity of 20 m/s. The static pressure in the duct is measured to be 100 kPa, and the air density is 1.2 kg/m^3. We want to find the stagnation pressure at this point in the flow.
Given: Flow velocity (V) = 20 m/s Static pressure (P) = 100 kPa = 100,000 Pa Density (ρ) = 1.2 kg/m^3
Using the formula for stagnation pressure:
P_0 = P + 0.5 * ρ * V^2
Substitute the given values:
P_0 = 100,000 Pa + 0.5 * 1.2 kg/m^3 * (20 m/s)^2
P_0 = 100,000 Pa + 0.5 * 1.2 kg/m^3 * 400 m^2/s^2
P_0 = 100,000 Pa + 240 kg/m^3 * m^2/s^2
P_0 = 100,000 Pa + 240 N/m^2
P_0 = 100,240 Pa
So, the stagnation pressure at the specified point in the flow is approximately 100,240 Pa, or 100.24 kPa.
In this example, we used the given flow velocity, static pressure, and air density to calculate the stagnation pressure at a particular location in the air duct. This value represents the total pressure at that point, accounting for both the static and dynamic pressures of the flow.
Formula table
Here's a table summarizing the formulas mentioned earlier for stagnation pressure and related parameters:
| Parameter | Symbol | Formula |
| Stagnation Pressure | P_0 | P + 0.5 * ρ * V^2 |
| Static Pressure | P | P_0 - 0.5 * ρ * V^2 |
| Dynamic Pressure | q | 0.5 * ρ * V^2 |
| Density | ρ (rho) | m / V |
| Flow Velocity | V | √(2 * q / ρ) |
| Mass Flow Rate | m_dot | A * ρ * V |
| Stagnation Temperature | T_0 | T + (V^2 / (2 * cp)) |
Where: P_0 = Stagnation Pressure (total pressure or pitot pressure) P = Static Pressure ρ = Density of the fluid V = Flow Velocity q = Dynamic Pressure (velocity pressure) A = Cross-sectional area of the flow m = Mass of the fluid T = Temperature of the fluid cp = Specific heat at constant pressure
These formulas are used in fluid mechanics, thermodynamics, aerodynamics, and other engineering fields to analyze fluid flow behavior, energy changes, and pressure distributions in fluid systems.
What is the significance of stagnation pressure?
The significance of stagnation pressure lies in its role as a fundamental concept in fluid mechanics and its practical applications in various engineering fields. Some of the key aspects of its significance are:
- Total Energy Measurement: Stagnation pressure represents the total energy content of a fluid stream. It includes both the static pressure (pressure due to fluid molecules' random motion) and the dynamic pressure (pressure due to the fluid's motion). This total energy measurement is essential in analyzing fluid flows and energy distribution within a system.
- Aerodynamics: In aerodynamics, stagnation pressure is crucial for analyzing aircraft and spacecraft performance. It is used to calculate airspeed, lift, and drag forces, and it provides critical data for optimizing wing design and aerodynamic efficiency.
- Gas Dynamics: In gas dynamics and propulsion systems, stagnation pressure plays a vital role in understanding the performance of jet engines, rockets, and nozzles. It helps determine the thrust generated and the overall efficiency of these propulsion systems.
- Wind Tunnel Testing: Stagnation pressure measurements are used in wind tunnel testing to evaluate the aerodynamic characteristics of models and prototypes. It allows engineers to simulate real-world conditions and assess how various objects interact with fluid flows.
- Fluid Flow Analysis: Stagnation pressure provides valuable insights into the behavior of fluid flow around obstacles, through pipes, or within complex geometries. It helps identify regions of high pressure, low pressure, and areas of separation or recirculation in the flow.
- Boundary Layer Analysis: In fluid dynamics, the boundary layer is the region of fluid flow close to a solid surface where viscosity effects are significant. Stagnation pressure measurements are used to study boundary layer thickness and its impact on drag and lift forces.
- Compressible Flows: Stagnation pressure is particularly important in compressible flows, where changes in fluid velocity and density significantly affect the flow behavior. It helps determine the critical points such as Mach number and shock waves.
- HVAC Systems: In heating, ventilation, and air conditioning (HVAC) systems, stagnation pressure measurements are used to assess airflow rates and pressure differentials in ducts and pipes.
- Fluid System Design: Engineers use stagnation pressure calculations to design efficient and safe fluid systems for various applications, such as pipelines, turbines, compressors, and heat exchangers.
- Research and Development: Stagnation pressure measurements are essential for researchers and scientists in various fields to study fluid behavior, investigate new technologies, and advance our understanding of fluid mechanics.
Overall, stagnation pressure provides a comprehensive and insightful way to understand fluid flow characteristics, energy changes, and pressure distributions in different engineering applications. Its significance extends across a wide range of industries and scientific disciplines, making it a fundamental concept in fluid dynamics and thermodynamics.
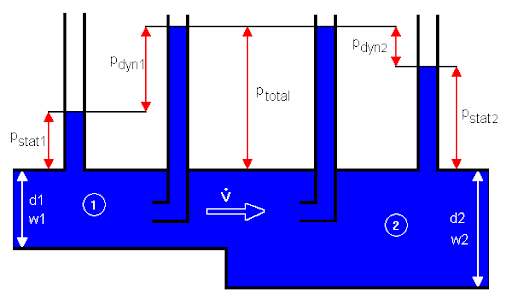
Fig 3. Pressures scale
Stagnation pressure different types
Stagnation pressure can be categorized into different types based on the specific context or application in which it is used. Here are some common types of stagnation pressure:
- Stagnation Pressure (Total Pressure): This is the most commonly referred to type of stagnation pressure. It represents the total energy contained in a fluid stream and includes both the static pressure and the dynamic pressure. It is also known as total pressure or pitot pressure.
- Stagnation Pressure in Compressible Flows: In compressible fluid flows, the term "stagnation pressure" is often used to refer to the total pressure (including both static and dynamic pressures). This is particularly relevant in supersonic flows where compressibility effects become significant.
- Stagnation Pressure in Incompressible Flows: In incompressible fluid flows, stagnation pressure typically refers to the total pressure as well. However, since the density remains nearly constant, the dynamic pressure contribution is usually much smaller than the static pressure contribution.
- Stagnation Pressure Rise: Stagnation pressure rise occurs when the stagnation pressure increases along a fluid flow due to various factors, such as compression or adiabatic heating.
- Stagnation Pressure Loss: Stagnation pressure loss happens when the stagnation pressure decreases along a fluid flow. This can occur due to factors like friction, shock waves, or expansion.
- Stagnation Pressure Recovery: Stagnation pressure recovery refers to the regaining of stagnation pressure after experiencing a pressure loss. For example, in some flow scenarios, the flow may expand after passing through a constriction, leading to a partial recovery of stagnation pressure.
- Stagnation Pressure Point: Stagnation pressure point is the specific location in a fluid flow where the flow velocity becomes zero, and the stagnation pressure reaches its maximum value. This is known as the stagnation or stagnation point.
These types of stagnation pressure are used in various engineering applications, such as aerodynamics, gas dynamics, and fluid mechanics, to analyze flow behavior, energy changes, and pressure distributions in fluid systems. The appropriate type of stagnation pressure used in a particular scenario depends on the nature of the flow and the specific parameters being analyzed.
-
Stagnation Pressure (Total Pressure)
Stagnation pressure, also known as total pressure or pitot pressure, represents the total energy contained in a fluid stream. It accounts for both the static pressure (pressure due to fluid molecules' random motion) and the dynamic pressure (pressure due to the fluid's motion). Stagnation pressure is a fundamental concept in fluid mechanics and is widely used in various engineering applications. It is denoted as P_0 and is expressed as:
P_0 = P + 0.5 * ρ * V^2
where P is the static pressure, ρ is the density of the fluid, and V is the flow velocity.
Stagnation Pressure in Compressible Flows: In compressible fluid flows, especially in situations where the fluid velocity approaches or exceeds the speed of sound, compressibility effects become significant. Stagnation pressure in such cases still refers to the total pressure, including both static and dynamic pressures. However, compressibility effects cause changes in the density and temperature of the fluid, leading to alterations in stagnation pressure distribution in the flow field.
Stagnation Pressure in Incompressible Flows: In incompressible fluid flows, the density remains nearly constant, and the fluid velocity is much lower than the speed of sound. As a result, the dynamic pressure contribution (0.5 * ρ * V^2) in the stagnation pressure formula is often much smaller than the static pressure contribution (P). In these flows, the term "stagnation pressure" typically still refers to the total pressure, but the dynamic pressure can sometimes be neglected due to its small magnitude.
-
Stagnation Pressure Rise
Stagnation pressure rise occurs when the stagnation pressure increases along a fluid flow. This can happen due to various factors, such as compression or adiabatic heating. For example, in a converging nozzle, the fluid is compressed, leading to a rise in the stagnation pressure.
Stagnation Pressure Loss: Stagnation pressure loss, also known as total pressure loss, happens when the stagnation pressure decreases along a fluid flow. This occurs due to factors such as friction, shock waves, or expansion. For instance, when a fluid flows through a diverging nozzle, it expands, leading to a loss in stagnation pressure.
Stagnation Pressure Recovery: Stagnation pressure recovery refers to the phenomenon where stagnation pressure partially recovers after experiencing a pressure loss. This recovery can occur under certain flow conditions, such as after passing through a constriction or a shock wave. For example, in some aerodynamic shapes, the flow downstream of a shock wave may experience partial stagnation pressure recovery due to the pressure wave's interaction with the flow.
-
Stagnation Pressure Point
Stagnation pressure point is a specific location in a fluid flow where the flow velocity becomes zero, and the stagnation pressure reaches its maximum value. This point is called the stagnation or stagnation point. For example, in aerodynamics, the stagnation point is the point where the fluid directly faces the oncoming flow and experiences maximum stagnation pressure. This occurs at the leading edge of an airfoil or the nose of an aircraft.
These different types of stagnation pressure concepts are essential in understanding fluid flow behavior, energy changes, and pressure distributions in various engineering applications, ranging from aircraft design to gas turbine performance analysis. The choice of the appropriate type depends on the specific flow conditions and parameters being analyzed.
Comparing table
Here's a comparison table summarizing the different types of stagnation pressure:
| Type of Stagnation Pressure | Definition | Formula |
| Stagnation Pressure | Total pressure in a fluid stream, including both static and dynamic pressures. | P_0 = P + 0.5 * ρ * V^2 |
| Stagnation Pressure in Compressible Flows | Total pressure in compressible fluid flows, where compressibility effects become significant. | P_0 = P + 0.5 * ρ * V^2 |
| Stagnation Pressure in Incompressible Flows | Total pressure in incompressible fluid flows, where the dynamic pressure contribution is small. | P_0 = P + 0.5 * ρ * V^2 |
| Stagnation Pressure Rise | Increase in stagnation pressure along a fluid flow, often due to compression or adiabatic heating. | Depends on the specific flow scenario and compressibility effects. |
| Stagnation Pressure Loss | Decrease in stagnation pressure along a fluid flow, caused by factors like friction or expansion. | Depends on the specific flow scenario and compressibility effects. |
| Stagnation Pressure Recovery | Partial regaining of stagnation pressure after a pressure loss, often seen after passing through a shock wave or constriction. | Depends on the specific flow scenario and compressibility effects. |
| Stagnation Pressure Point | Specific location in a fluid flow where the flow velocity becomes zero, and the stagnation pressure reaches its maximum value. | Occurs at the stagnation or stagnation point, often at the leading edge of an airfoil. |
The table provides a quick comparison of the different types of stagnation pressure, highlighting their definitions and any unique characteristics. These types are used in various engineering applications to analyze fluid flow behavior, energy changes, and pressure distributions in fluid systems under different flow conditions.
What is stagnation pressure used for?
Stagnation pressure, also known as total pressure or pitot pressure, is used for various purposes in fluid mechanics, thermodynamics, and engineering applications. Some of the key uses of stagnation pressure include:
- Airspeed Measurement: Stagnation pressure is crucial for determining the airspeed of an aircraft. By measuring the stagnation pressure using a Pitot tube, pilots can accurately gauge the aircraft's velocity relative to the surrounding air.
- Aerodynamic Analysis: Stagnation pressure helps in the analysis of aerodynamic characteristics, lift, and drag forces on objects such as airfoils, wings, and vehicles. It aids in designing efficient and stable flying vehicles.
- Wind Tunnel Testing: In wind tunnel experiments, stagnation pressure measurements are used to study and analyze the aerodynamic behavior of scaled-down models. This data provides insights into real-world applications and design improvements.
- Gas Turbines and Jet Engines: Stagnation pressure is essential for assessing the performance and efficiency of gas turbines, jet engines, and rocket nozzles. It helps optimize engine design and analyze thrust and exhaust gas behavior.
- Flow Behavior Analysis: Stagnation pressure data is used to analyze the behavior of fluid flows around obstacles, through pipes, and within complex geometries. It helps identify regions of high pressure, low pressure, and areas of flow separation or recirculation.
- Boundary Layer Studies: Stagnation pressure measurements are used to study boundary layer characteristics near solid surfaces. Understanding boundary layer behavior is vital in optimizing aerodynamic performance and reducing drag.
- HVAC Systems: In heating, ventilation, and air conditioning (HVAC) systems, stagnation pressure measurements are used to assess airflow rates and pressure differentials in ducts and pipes, ensuring efficient HVAC operations.
- Supersonic and Hypersonic Flows: In supersonic and hypersonic flow regimes, stagnation pressure is critical for analyzing shock waves, expansion waves, and other compressibility effects.
- Atmospheric Studies: Stagnation pressure measurements are utilized in meteorology to determine wind speed and direction and analyze weather patterns.
- Research and Development: Stagnation pressure data aids researchers and scientists in various fields to study fluid behavior, investigate new technologies, and advance the understanding of fluid mechanics.
In summary, stagnation pressure is a fundamental concept with diverse applications across numerous engineering disciplines. Its role in aerodynamics, gas dynamics, propulsion, and fluid analysis makes it a critical parameter for understanding and optimizing the behavior of fluid systems in both real-world applications and research settings.
How is stagnation pressure different from static pressure?
Stagnation pressure and static pressure are two important concepts in fluid mechanics that represent different aspects of the pressure in a fluid flow. They are related but have distinct characteristics:
- Stagnation Pressure: Stagnation pressure, also known as total pressure or pitot pressure, is the total energy contained in a fluid stream. It accounts for both the static pressure and the dynamic pressure of the flow. Stagnation pressure represents the maximum pressure that the fluid would achieve if it were brought to a complete stop, adiabatically (without any heat transfer) and isentropically (without any entropy change). It is the pressure measured when the fluid comes to rest due to compression and is usually measured using a Pitot tube or similar devices.
Formula for Stagnation Pressure (P_0): P_0 = P + 0.5 * ρ * V^2
where: P_0 = Stagnation Pressure (total pressure) P = Static Pressure ρ = Density of the fluid V = Flow Velocity
- Static Pressure: Static pressure is the pressure exerted by fluid molecules in random motion. It represents the pressure at a given point in the fluid flow when the fluid is in motion. It does not consider the kinetic energy of the flow and is the pressure measured when the fluid is not flowing (i.e., at rest). Static pressure is crucial in determining the balance of forces in fluid systems and is used in various engineering applications, such as in designing pressure vessels, calculating loads on surfaces, and determining fluid velocities.
Static Pressure Formula: P = P_0 - 0.5 * ρ * V^2
where: P = Static Pressure P_0 = Stagnation Pressure (total pressure) ρ = Density of the fluid V = Flow Velocity
Key Differences:
Components of Pressure: Stagnation pressure includes both the static pressure and the dynamic pressure (0.5 * ρ * V^2), while static pressure considers only the pressure due to fluid molecules' random motion.
Total Energy vs. Local Energy: Stagnation pressure represents the total energy contained in the fluid stream, accounting for the fluid's kinetic energy. Static pressure, on the other hand, represents the local energy at a specific point in the flow.
Flow Conditions: Stagnation pressure is relevant when the fluid flow is in motion, whereas static pressure is relevant whether the fluid is in motion or at rest.
Both stagnation pressure and static pressure are important parameters used in various engineering applications to analyze fluid flow behavior, pressure distributions, and energy changes within fluid systems. Understanding the differences between these pressure types is crucial for accurately assessing fluid dynamics in practical scenarios.
Can stagnation pressure be higher than the static pressure?
Yes, stagnation pressure can be higher than the static pressure in a fluid flow. In fact, this is a common occurrence in various fluid dynamics scenarios.
Stagnation pressure (P_0) is the total pressure in a fluid stream, accounting for both the static pressure (P) and the dynamic pressure (0.5 * ρ * V^2), where ρ is the density of the fluid, and V is the flow velocity.
The dynamic pressure component (0.5 * ρ * V^2) is directly related to the flow velocity and represents the pressure due to the fluid's motion. As the flow velocity increases, the dynamic pressure increases proportionally.
If the flow velocity is high enough, the dynamic pressure can significantly contribute to the stagnation pressure, resulting in a higher total pressure (P_0) compared to the static pressure (P).
This situation is common in high-speed flows, such as supersonic or hypersonic flows, where the fluid's velocity approaches or exceeds the speed of sound. In these scenarios, the dynamic pressure can become dominant, leading to a substantial difference between the stagnation pressure and the static pressure.
For example, in a supersonic aircraft flying at high speeds, the stagnation pressure at the aircraft's nose can be significantly higher than the static pressure measured at the surrounding atmospheric conditions.
In summary, stagnation pressure can indeed be higher than static pressure, especially in high-speed flows where the dynamic pressure plays a significant role in the total pressure calculation.
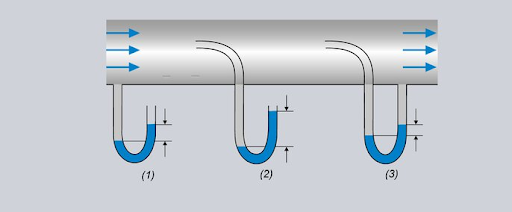
Fig 4. Flow measurement
Is stagnation pressure constant in a flow field?
In an ideal, adiabatic, and isentropic flow, stagnation pressure remains constant along a streamline. This condition is often referred to as "stagnation pressure conservation."
Stagnation pressure conservation is based on the Bernoulli's principle, which states that the total mechanical energy per unit mass of a fluid particle remains constant along a streamline in the absence of external work and heat transfer. In other words, if a fluid particle follows a streamline without any energy exchange with its surroundings, the sum of its static pressure and dynamic pressure (stagnation pressure) will remain constant.
In real-world scenarios, however, there are various factors that can cause the stagnation pressure to change along a flow field. Some of the reasons for stagnation pressure variation include:
- Friction: Friction between the fluid and the surfaces it flows over can cause energy losses and lead to a decrease in stagnation pressure.
- Heat Transfer: If heat is exchanged between the fluid and its surroundings, adiabatic conditions are not met, and stagnation pressure may be affected.
- Compressibility: In compressible flows, such as those with shock waves or regions of high Mach numbers, the conservation of stagnation pressure may not hold.
- Expansion or Compression: Changes in flow area can cause changes in the fluid's velocity and, consequently, its stagnation pressure.
- Turbulence: Turbulent flows can have significant energy fluctuations, impacting stagnation pressure.
- Viscosity: Viscous effects in the fluid can cause energy losses, affecting the stagnation pressure.
In practice, it is essential to consider these factors and the specific flow conditions to determine whether stagnation pressure remains constant or varies along a flow field. While stagnation pressure conservation is an essential concept in fluid mechanics, it is an idealized condition and may not hold in all real-world scenarios.
Why is stagnation pressure important in aerodynamics?
Stagnation pressure is of paramount importance in aerodynamics due to its fundamental role in understanding and analyzing the airflow around objects, such as aircraft, rockets, and other flying vehicles. Here are some key reasons why stagnation pressure is significant in aerodynamics:
- Airspeed Measurement: Stagnation pressure is directly related to the airspeed of an aircraft. By measuring the stagnation pressure using a Pitot tube, the airspeed can be determined. This critical information is essential for pilots to ensure safe and optimal flight operations.
- Lift and Drag Calculations: Understanding the stagnation pressure distribution around an airfoil or wing helps aerodynamicists calculate lift and drag forces. The difference in stagnation pressure between the upper and lower surfaces of the wing contributes to lift generation, while the stagnation pressure on the aircraft's nose affects drag forces.
- Aerodynamic Efficiency: Stagnation pressure analysis enables the assessment of an aircraft's aerodynamic efficiency. By optimizing the pressure distribution on the aircraft's surfaces, designers can improve fuel efficiency and performance.
- Flow Separation and Stall Prediction: Stagnation pressure measurements provide insights into flow separation and stall conditions. Studying stagnation pressure patterns can help identify regions of potential flow separation, which is crucial for preventing dangerous stall situations.
- Shock Wave Analysis: In supersonic and hypersonic flows, stagnation pressure is essential for analyzing shock waves. Shock waves are regions of abrupt pressure and density changes and have a significant impact on aerodynamic performance.
- Boundary Layer Studies: Stagnation pressure measurements are used to study boundary layer characteristics. The boundary layer is the thin layer of fluid near a solid surface, and its behavior significantly affects aerodynamic forces and drag.
- Wind Tunnel Testing: In wind tunnel experiments, stagnation pressure is measured to assess airflow behavior around scaled-down models of aircraft and other objects. These tests provide valuable data for design improvements and validating aerodynamic theories.
- Performance Optimization: Stagnation pressure analysis allows engineers to optimize aircraft and spacecraft designs, reducing drag, improving lift, and achieving better overall performance.
- Mach Number Determination: Stagnation pressure is used to determine the Mach number, a dimensionless parameter that indicates the speed of an aircraft relative to the speed of sound in the surrounding air.
Overall, stagnation pressure plays a central role in aerodynamics by providing critical data for designing and analyzing flying vehicles' performance. The understanding of stagnation pressure and its distribution aids in achieving safe, efficient, and high-performance flight operations.
What is the relationship between stagnation pressure and Bernoulli's principle?
Stagnation pressure and Bernoulli's principle are closely related concepts in fluid mechanics. Bernoulli's principle is a fundamental principle that describes the behavior of an ideal fluid in steady flow. The relationship between stagnation pressure and Bernoulli's principle can be understood through the application of the principle along a streamline.
Bernoulli's principle states that in an ideal, steady, and incompressible flow, the total mechanical energy per unit mass of the fluid remains constant along a streamline. This total mechanical energy includes three components: the fluid's potential energy (due to its elevation), the fluid's kinetic energy (due to its motion), and the fluid's pressure energy.
The equation for Bernoulli's principle along a streamline is as follows:
P + 0.5 * ρ * V^2 + ρ * g * h = constant
where: P is the static pressure of the fluid, ρ is the density of the fluid, V is the flow velocity, g is the acceleration due to gravity, h is the height above a reference plane.
Now, consider the case where the fluid is brought to rest adiabatically (without any heat transfer) and isentropically (without any entropy change). At this point, the fluid's kinetic energy becomes zero (V = 0), and the equation simplifies to:
P + ρ * g * h = constant
This constant value represents the stagnation pressure (P_0) of the fluid. Thus, we can say that in an adiabatic and isentropic flow where the fluid comes to rest, the stagnation pressure is equal to the sum of the static pressure and the hydrostatic pressure (ρ * g * h).
In summary, the relationship between stagnation pressure and Bernoulli's principle is that the stagnation pressure is the total mechanical energy per unit mass of the fluid when it comes to rest adiabatically and isentropically along a streamline. It is a direct consequence of Bernoulli's principle applied to this specific scenario.
How is stagnation pressure affected by an increase in flow velocity?
Stagnation pressure is directly affected by an increase in flow velocity. As the flow velocity increases, the stagnation pressure also increases.
Stagnation pressure (P_0) is the total pressure in a fluid stream and is given by the sum of the static pressure (P) and the dynamic pressure (0.5 * ρ * V^2), where ρ is the density of the fluid, and V is the flow velocity.
The dynamic pressure component (0.5 * ρ * V^2) represents the pressure due to the fluid's motion. It is directly proportional to the square of the flow velocity. Therefore, as the flow velocity increases, the dynamic pressure increases much faster.
The relationship between flow velocity and stagnation pressure is described by the stagnation pressure formula:
P_0 = P + 0.5 * ρ * V^2
When the flow velocity (V) increases, the dynamic pressure term (0.5 * ρ * V^2) becomes larger, resulting in a higher stagnation pressure (P_0). Conversely, if the flow velocity decreases, the dynamic pressure decreases, leading to a lower stagnation pressure.
This relationship is important in various engineering applications. For example, in aerodynamics, an increase in flow velocity can result in higher stagnation pressure at specific points on an airfoil or aircraft. Similarly, in gas turbine engines, an increase in airflow velocity can lead to higher stagnation pressure at the engine inlet, affecting the engine's performance.
In summary, an increase in flow velocity results in a higher stagnation pressure, while a decrease in flow velocity leads to a lower stagnation pressure. Understanding this relationship is crucial for analyzing fluid flow behavior and its impact on pressure distributions in various engineering applications.
What are parameters affect on stagnation pressure?
Stagnation pressure is affected by several parameters that influence the fluid flow behavior. These parameters include:
- Flow Velocity (V): Stagnation pressure is directly proportional to the square of the flow velocity. As the flow velocity increases, the dynamic pressure component (0.5 * ρ * V^2) in the stagnation pressure formula becomes larger, resulting in higher stagnation pressure.
- Static Pressure (P): Stagnation pressure is the sum of the static pressure and dynamic pressure. An increase in static pressure will lead to a corresponding increase in stagnation pressure.
- Density of the Fluid (ρ): Stagnation pressure is directly proportional to the density of the fluid. Higher fluid density will result in higher stagnation pressure for the same flow conditions.
- Compressibility Effects: In compressible flows, especially in high-speed flows where the fluid velocity approaches or exceeds the speed of sound, compressibility effects become significant. These effects can alter the stagnation pressure distribution and may lead to changes in the flow behavior.
- Flow Area (A): Changes in the cross-sectional area of the flow path can affect the flow velocity and, consequently, the stagnation pressure. For example, a converging section may increase the flow velocity and raise the stagnation pressure.
- Temperature (T): Changes in temperature can affect the density of the fluid, which, in turn, influences the stagnation pressure. For ideal gases, the relationship between temperature and density is described by the ideal gas law (ρ = P / (R * T)), where R is the gas constant.
- Fluid Properties: Different fluids have varying densities and specific heat capacities, affecting the stagnation pressure for the same flow conditions.
- Boundary Layer Effects: In fluid flow near solid surfaces, the boundary layer affects the fluid's behavior. This can lead to changes in the stagnation pressure distribution along the surface.
- Flow Regime: Stagnation pressure can be influenced by the flow regime, such as laminar or turbulent flow. Turbulent flows may have higher energy losses and lead to variations in stagnation pressure.
- Obstacles and Flow Obstructions: Presence of obstacles or flow obstructions in the fluid path can cause pressure changes, influencing the stagnation pressure at specific locations.
- Heat Transfer: Stagnation pressure can be affected by heat transfer processes in the fluid, especially if the flow is not adiabatic.
Understanding these parameters and their effects on stagnation pressure is crucial for analyzing fluid flow behavior, optimizing aerodynamic designs, and predicting the performance of various fluid systems.
What happens to stagnation pressure when fluid flows through a nozzle?
When a fluid flows through a nozzle, the stagnation pressure typically decreases. This phenomenon is known as "stagnation pressure loss" or "total pressure loss" and occurs due to the conversion of stagnation pressure into kinetic energy as the flow accelerates through the nozzle.
In a nozzle, the cross-sectional area decreases in the flow direction, leading to an increase in flow velocity according to the principle of continuity (mass conservation). As the fluid accelerates, its kinetic energy increases, and this energy is taken from the stagnation pressure.
The process of pressure decrease in a nozzle can be explained by the conservation of energy. According to Bernoulli's principle, the total mechanical energy per unit mass of the fluid remains constant along a streamline in an ideal, steady, and incompressible flow. In the nozzle, as the flow velocity increases, the kinetic energy component (0.5 * ρ * V^2) in the stagnation pressure formula becomes larger, resulting in a decrease in stagnation pressure.
The decrease in stagnation pressure is usually more significant in converging nozzles, where the cross-sectional area decreases continuously. This reduction in pressure allows the fluid to maintain energy conservation throughout the flow.
Stagnation pressure loss in a nozzle is a crucial consideration in various engineering applications, such as in gas turbine engines, rocket nozzles, and fluid systems with constricted flow passages. Engineers need to account for the pressure loss to optimize system performance and design efficient nozzles for specific purposes.
How does stagnation pressure relate to the concept of stagnation point in fluid mechanics?
Stagnation pressure and the concept of a stagnation point in fluid mechanics are closely related and interconnected.
The Stagnation Point: A stagnation point is a specific location in a fluid flow where the flow velocity becomes zero (V = 0). At this point, the fluid comes to rest due to an obstacle or flow constriction, and the velocity energy is converted entirely into pressure energy. As a result, the pressure at the stagnation point reaches its maximum value, known as stagnation pressure (P_0).
The Stagnation Pressure: Stagnation pressure (P_0) is the total pressure in a fluid stream and represents the maximum pressure that the fluid would achieve if it were brought to a complete stop adiabatically (without any heat transfer) and isentropically (without any entropy change). Stagnation pressure accounts for both the static pressure (P) and the dynamic pressure (0.5 * ρ * V^2) of the fluid.
The Relationship: The relationship between stagnation pressure and the concept of a stagnation point is evident in their definitions. At the stagnation point, the fluid's velocity is zero, and all its kinetic energy is converted into pressure energy. Therefore, the pressure at the stagnation point is the maximum in the fluid flow, representing the stagnation pressure (P_0).
Mathematically, at the stagnation point:
V = 0 Dynamic Pressure (0.5 * ρ * V^2) = 0
As a result, the stagnation pressure formula simplifies to:
P_0 = P
This means that at the stagnation point, the stagnation pressure (P_0) is equal to the static pressure (P). The pressure at any other point in the flow (away from the stagnation point) will be lower than the stagnation pressure due to the presence of flow velocity and dynamic pressure.
In summary, the concept of a stagnation point is related to stagnation pressure in fluid mechanics. The stagnation point represents the location where the fluid velocity is zero, and the pressure reaches its maximum value, which is equal to the stagnation pressure. Understanding the behavior of the flow at the stagnation point and the associated stagnation pressure is crucial for analyzing fluid flow around obstacles, airfoils, and other fluid systems.
What is the impact of friction on stagnation pressure in a fluid flow?
Friction in a fluid flow has a significant impact on the stagnation pressure. As the fluid interacts with surfaces and experiences viscosity, energy losses occur due to fluid-solid interactions, resulting in a decrease in stagnation pressure. This phenomenon is known as "stagnation pressure loss" or "total pressure loss" due to friction.
When a fluid flows over a surface, the fluid molecules in direct contact with the surface experience drag and shear forces. This interaction causes energy dissipation in the form of heat, resulting in a loss of mechanical energy. As a consequence, the fluid's total pressure (stagnation pressure) decreases compared to what it would be in an ideal, frictionless flow.
The extent of stagnation pressure loss due to friction depends on several factors, including the following:
- Flow Velocity: Higher flow velocities lead to higher frictional losses, as the fluid interacts more intensely with the surfaces it flows over.
- Viscosity of the Fluid: Fluids with higher viscosity experience stronger internal friction, resulting in more significant stagnation pressure losses.
- Surface Roughness: Rough surfaces introduce additional frictional effects, causing higher energy losses in the fluid flow.
- Flow Path Geometry: The shape and curvature of the flow path affect the magnitude of frictional losses.
- Reynolds Number: The Reynolds number, which characterizes the flow regime, influences the level of turbulence and laminar flow. Turbulent flows generally experience higher frictional losses than laminar flows.
- Flow Distance: The distance the fluid travels over the surface affects the cumulative effect of friction on the stagnation pressure.
Stagnation pressure loss due to friction is particularly relevant in real-world fluid systems, where ideal conditions are not achieved. In practical engineering applications, it is essential to account for these pressure losses when designing and analyzing fluid flow systems, such as pipelines, ducts, heat exchangers, and other components.
Understanding the impact of friction on stagnation pressure is crucial for accurately predicting the behavior of fluid systems and ensuring efficient and reliable operation in various engineering applications.
How does stagnation pressure change across a shock wave?
Across a shock wave, the stagnation pressure undergoes a significant change. A shock wave is a high-intensity compression wave that occurs when a fluid flows at a supersonic speed and encounters a sudden change in flow conditions, such as a constriction or an object. As the fluid passes through the shock wave, the stagnation pressure experiences a sudden increase, resulting in a phenomenon known as "stagnation pressure rise."
The key changes in stagnation pressure across a shock wave can be understood by considering the conservation of energy and momentum in the flow:
- Stagnation Pressure Rise: When a fluid encounters a shock wave, its flow velocity abruptly decreases to subsonic speed. This reduction in velocity causes a sudden increase in the static pressure, resulting in a rise in stagnation pressure. The increase in stagnation pressure is due to the conversion of the fluid's kinetic energy into pressure energy as it slows down across the shock wave.
- Flow Deceleration: As the fluid crosses the shock wave, it decelerates from supersonic to subsonic speed. This deceleration is associated with a corresponding increase in the static pressure and, consequently, the stagnation pressure.
- Temperature Rise: Shock waves cause an increase in fluid temperature, which is linked to the rise in stagnation pressure. The shock wave compresses the fluid and converts some of the flow's kinetic energy into thermal energy, leading to an increase in temperature and pressure.
It's essential to note that the change in stagnation pressure across a shock wave is not reversible. Once the flow passes through the shock, the pressure rise is permanent, and the fluid remains at a higher stagnation pressure downstream of the shock wave.
Stagnation pressure changes across shock waves play a critical role in aerodynamics, gas dynamics, and supersonic/hypersonic flows. These changes can significantly impact the performance and behavior of various aerodynamic shapes, aircraft, and propulsion systems. Understanding the effects of shock waves on stagnation pressure is essential for designing high-speed vehicles, wind tunnels, and other engineering systems involving compressible fluid flows.
What is the impact of stagnation pressure on boundary layer separation?
Stagnation pressure can have a significant impact on boundary layer separation in fluid flows. Boundary layer separation occurs when the boundary layer, which is the thin layer of fluid adjacent to a solid surface, detaches from the surface and forms a separated flow region. The presence of stagnation pressure gradients can influence the occurrence and extent of boundary layer separation.
- Boundary Layer Acceleration: In regions with favorable pressure gradients, where the stagnation pressure increases in the flow direction, the boundary layer tends to accelerate along the surface. This acceleration helps to maintain attachment of the boundary layer to the surface, delaying or preventing separation.
- Boundary Layer Deceleration: In regions with adverse pressure gradients, where the stagnation pressure decreases in the flow direction, the boundary layer experiences deceleration. This deceleration can lead to flow separation, where the boundary layer separates from the surface, creating a separated flow region.
- Separation Bubble: In some cases, the combination of favorable and adverse pressure gradients can lead to the formation of a separation bubble. A separation bubble occurs when the boundary layer initially separates from the surface due to an adverse pressure gradient but reattaches further downstream due to a favorable pressure gradient. This creates a recirculation zone within the separation bubble.
- Flow Reattachment: Stagnation pressure gradients can also influence flow reattachment after separation. In cases where the pressure gradient becomes favorable again, the separated flow region may reattach to the surface, reducing the size and intensity of the separated region.
- Impact on Lift and Drag: Boundary layer separation has a direct impact on the aerodynamic forces acting on an object, such as an airfoil or wing. Separation can significantly increase drag and reduce lift, affecting the overall aerodynamic performance of the object.
- Flow Control: Understanding the impact of stagnation pressure on boundary layer separation is essential for flow control strategies. By manipulating the pressure distribution, engineers can design aerodynamic shapes and control surfaces to delay separation or promote reattachment, enhancing the efficiency and stability of vehicles.
In summary, stagnation pressure gradients play a crucial role in boundary layer behavior and separation. Proper management of stagnation pressure distributions can be used to control boundary layer separation and improve the aerodynamic performance of various engineering systems, such as aircraft, vehicles, and turbines.
Conclusion
In conclusion, stagnation pressure is a fundamental concept in fluid mechanics that represents the total pressure in a fluid stream, accounting for both the static pressure and the dynamic pressure due to the fluid's motion. It is measured when the fluid comes to rest adiabatically and isentropically, and it plays a crucial role in various engineering applications.
Stagnation pressure is used for a wide range of purposes, including airspeed measurement, aerodynamic analysis, wind tunnel testing, gas turbine and jet engine performance assessment, flow behavior analysis, boundary layer studies, and atmospheric studies.
Several parameters affect stagnation pressure, including flow velocity, static pressure, fluid density, compressibility effects, flow area, temperature, and friction. Understanding these parameters is essential for accurately predicting fluid behavior in different flow scenarios.
Stagnation pressure is related to the concept of a stagnation point in fluid mechanics. At the stagnation point, the fluid velocity is zero, and the pressure reaches its maximum value, which is equal to the stagnation pressure. Stagnation pressure loss due to friction is an important consideration in real-world fluid systems, leading to a decrease in stagnation pressure as the fluid interacts with surfaces and experiences energy losses.
Furthermore, across a shock wave, stagnation pressure undergoes a significant change, experiencing a sudden increase known as "stagnation pressure rise." Stagnation pressure changes can influence boundary layer separation, affecting aerodynamic performance and flow control strategies in various engineering applications.
Overall, understanding stagnation pressure and its effects on fluid flow behavior is essential for optimizing system design, predicting performance, and ensuring safe and efficient operation in numerous engineering and scientific disciplines.
To recap
- Q: What is stagnation pressure?
A: Stagnation pressure, also known as total pressure or pitot pressure, is the total energy contained in a fluid stream. It represents the pressure the fluid would have if brought to rest adiabatically and isentropically.
- Q: How is stagnation pressure measured?
A: Stagnation pressure is often measured using a device called a Pitot tube, which has a forward-facing opening to measure the total pressure and a side opening to measure the static pressure. The stagnation pressure is then calculated as the sum of the total pressure and the dynamic pressure.
- Q: What are the factors affecting stagnation pressure?
A: Stagnation pressure is affected by flow velocity, static pressure, fluid density, compressibility effects, flow area, temperature, friction, boundary layer behavior, and flow regime.
- Q: Can stagnation pressure be higher than static pressure?
A: Yes, stagnation pressure can be higher than static pressure, especially in high-speed flows where the dynamic pressure contributes significantly to the total pressure.
- Q: What is the relationship between stagnation pressure and Bernoulli's principle?
A: Stagnation pressure is related to Bernoulli's principle, as it represents the total mechanical energy per unit mass of the fluid when it comes to rest along a streamline.
- Q: How is stagnation pressure affected by an increase in flow velocity?
A: Stagnation pressure increases with an increase in flow velocity, as the dynamic pressure component in the stagnation pressure formula becomes larger.
- Q: What happens to stagnation pressure when fluid flows through a nozzle?
A: Stagnation pressure decreases when fluid flows through a nozzle due to the conversion of stagnation pressure into kinetic energy as the flow accelerates.
- Q: How does stagnation pressure change across a shock wave?
A: Across a shock wave, stagnation pressure experiences a sudden increase known as "stagnation pressure rise" due to the abrupt decrease in flow velocity.
- Q: What is the impact of stagnation pressure on boundary layer separation?
A: Stagnation pressure gradients can influence boundary layer separation, affecting flow acceleration, deceleration, separation bubbles, and flow reattachment.
- Q: What is the significance of stagnation pressure in aerodynamics?
A: Stagnation pressure is crucial in aerodynamics for airspeed measurement, lift and drag calculations, aerodynamic efficiency analysis, flow separation prediction, shock wave analysis, and wind tunnel testing. It plays a central role in designing and optimizing aircraft and other flying vehicles.
Reference
https://www.mechnflow.com/post/total-pressure-static-pressure-and-dynamic-pressure
https://pipe-flo.com/static-pressure-stagnation-pressure/
http://www.pressure-drop.com/help/dynamic-pressure-change.html
https://www.differencebetween.info/difference-between-static-and-dynamic-pressure
Recent Posts
-
From Lab to Launchpad: Pressure Sensor Industry Certifications
In the intricate world of technology and precision engineering, where every measurement matters a …16th Mar 2024 -
Stand Out, Stand Certified: The Art of Pressure Sensor Safety
Stand Out, Stand Certified: The Art of Pressure Sensor Safety Welcome to the world of performance …9th Mar 2024 -
Robotics in Food and beverage Industry
Our lives depend on the food and beverage industry and it is in a constant state of evolution, …5th Mar 2024




